PostgreSQL

Appearance

什么是 B 树索引？ ​

通过不断分裂，建立一个矮胖型的平衡链表数据结构，

以下是一课B+树索引图

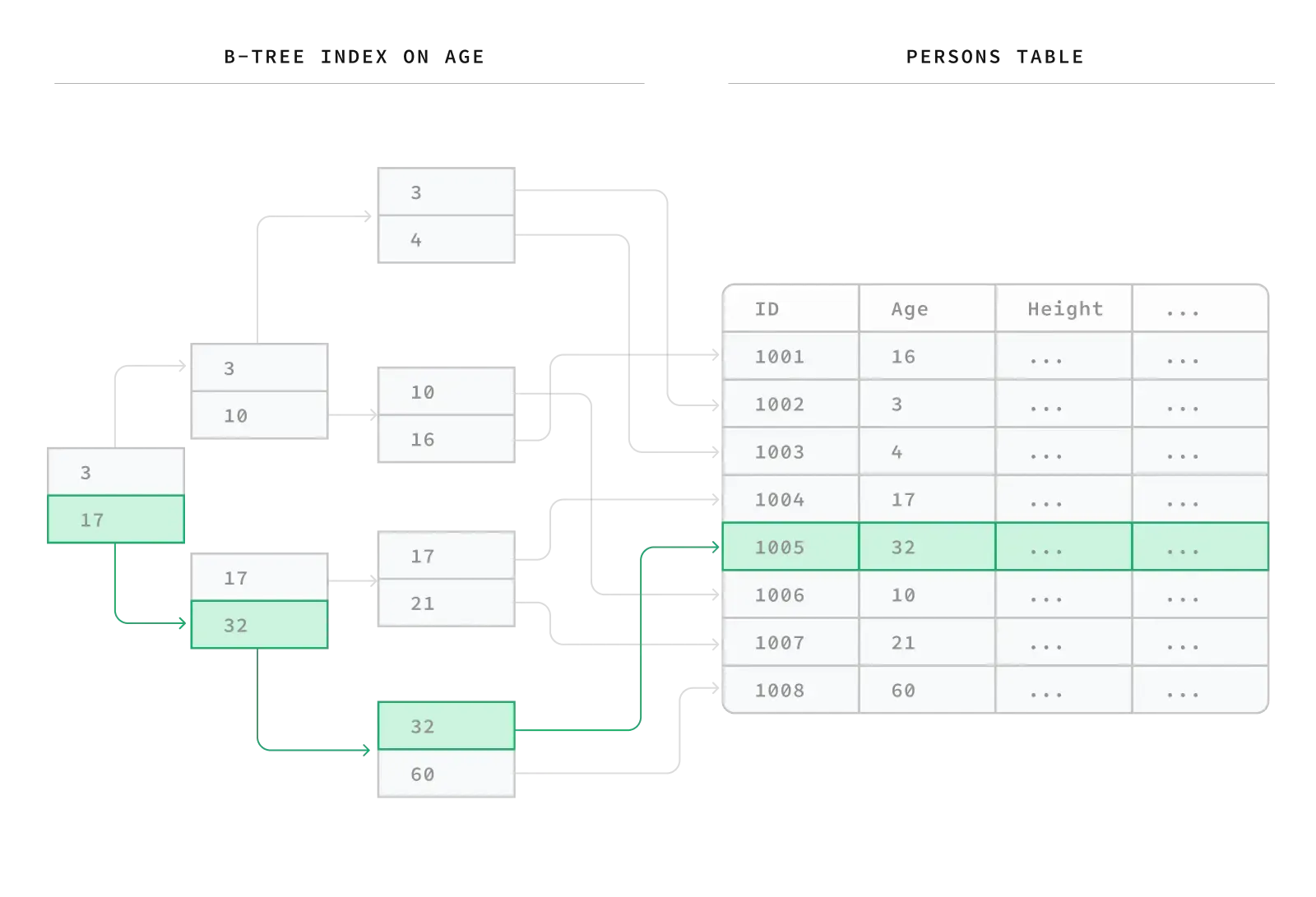
B+tree

B-树（B-Tree）是“平衡树”（Balanced Tree）的缩写，是数据库中最常用的一种索引类型。• 数据是有序的：B-树中的所有数据都是按顺序排列的，这使得范围查询（比如查找年龄在 20 到 30 岁之间的人）和精确查找都非常高效。• 它是平衡的：树的所有叶子节点都在同一层级。这保证了从树的顶部到底部查找任何一个数据，所花费的时间都差不多是相同的，查询性能非常稳定。

B-树的结构 ​

根节点 (Root Node)：树的最顶端节点。[3, 17] 分支节点 (Branch Nodes)：连接根节点和叶子节点的中间节点。 叶子节点 (Leaf Nodes)：树的最底层的节点。它们包含了索引列的值（这里是age）以及一个指向原始数据表中对应行的指针。

查询示例 ​

如何查找年龄为 32 的人？SELECT * FROM persons WHERE age = 32;

  1. 从根节点开始：查询从最顶层的根节点开始。根节点告诉你，比 17 小的值往左边的分支走。大于等于 17 的值往右边的分支走。因为 32 大于 17，所以我们沿着右边的路径向下。
  2. 来到分支节点：我们来到了一个分支节点，它包含 [17, 32]。这个节点告诉我们，值在 17 和 32 之间的向左走，大于等于 32 的向右走。因为我们要找的是 32，所以我们继续向右。
  3. 到达叶子节点：我们最终到达了一个叶子节点（最后一层），它包含 [32, 60]。在这里，我们找到了 32 这条记录。
  4. **回表：**这个叶子节点不仅存了 32 这个值，还存了一个指向 PERSONS TABLE 中实际数据行的指针。通过这个指针，数据库就能立刻定位到 ID 为 1005 的那一行数据，然后将整行数据返回给你。

核心思想 ​

B-树的核心思想是：“与其构建一棵又高又瘦的树，不如构建一棵又矮又胖的树。”

  • 高瘦的树（比如二叉搜索树）：每次只能做二选一的决定，如果数据量巨大，这棵树会变得非常高，从上走到下要经过很多层，查询效率会变差。
  • 矮胖的树（B-树）：在一个节点里存放多个值（路标），让你一次可以做**“多选一”**的决定。这样树的高度会大大降低，查询时从上到下经过的节点数会变得非常少，所以速度极快。

B-树的硬性规则 (算法的基石) ​

为了实现“矮胖”这个目标，B-树有几条必须遵守的铁律。

  1. 节点内元素有序
  2. 子节点的值范围被严格限定
  3. 所有叶子节点都在同一层：这是 “平衡” (Balanced) 的精髓，不管从根节点出发走哪条路，到达最底层的叶子节点所经过的层数是完全一样的。这保证了查询性能的稳定。
  4. 节点不能太“空”，也不能太“满”：除了根节点，每个节点里的值的数量不能少于 m/2 - 1，也不能超过 m-1。这保证了树的“矮胖”特性，不会浪费太多空间。

B-树算法的核心操作：插入与分裂 ​

B+tree

这棵B树的生成过程 (以上图为例)

B树是通过**自下而上的“分裂”和“提拔”**来生长的。我们假设这张表的最大容量是每个节点只能放2个值（这在学术上称为“3阶B树”），一旦要放第3个，节点就必须分裂。

我们按一个可能的顺序插入age列的数据：3, 4, 10, 16, 17, 21, 32, 60

第1步：插入 3, 4

  • 第一个节点（根节点，也是叶子节点）被创建。
  • 插入3 -> [3]
  • 插入4 -> [3, 4] (节点满了)

第2步：插入 10 (第一次分裂)

  • 尝试将10插入[3, 4]，节点临时变为[3, 4, 10]，超载了！

  • 触发分裂算法：

    1. 取中间值4。
    2. 将4提拔上去，成为一个新的根节点。
    3. 4左边的3成为左子节点，4右边的10成为右子节点。

  • 树的结构变为：

          [4]
     /   \\
   [3]   [10]

第3步：插入 16

  • 从根节点[4]开始，16 > 4，走右边。
  • 将16插入到[10]节点，变为[10, 16] (节点满了)。

第4步：插入 17 (第二次分裂，也是形成我们图中结构的关键一步)

  • 从根[4]开始，17 > 4，走右边，找到[10, 16]节点。

  • 尝试将17插入，节点临时变为[10, 16, 17]，超载！

  • 触发分裂算法：

    1. 取中间值16。
    2. 将16提拔到父节点[4]中。父节点变为[4, 16]。
    3. 旧节点[10, 16, 17]分裂成两个新节点[10]和[17]。

  • 树的结构变为：

         [4, 16]
    /   |   \\
  [3]  [10]  [17]

第5步：插入 21, 32, 60... (后续的分裂)

  • 插入21：21 > 16，进入[17]节点 -> [17, 21] (满了)
  • 插入32：尝试放入[17, 21]，临时[17, 21, 32]，超载！
    • 中间值21被提拔到父节点[4, 16]，父节点临时变为[4, 16, 21]，父节点也超载了！
    • 父节点也分裂！ 这就是所谓的连锁分裂，是B树生长的核心。
    • 父节点[4, 16, 21]的中间值16（或17，取决于实现细节，我们按图中结果反推，是17被提拔了）被提拔为新的根。
    • 这个过程持续下去，最终就会形成图中所示的结构。

总结一下生成逻辑：

  1. 数据总是被插入到最底层的叶子节点。
  2. 当一个叶子节点满了，它会分裂成两个，并把中间的那个值“提拔”到上一层的父节点中。
  3. 如果父节点也满了，父节点也会分裂，再把中间值向更上一层提拔。
  4. 这个过程可以一直持续到根节点，如果根节点也分裂了，那么整棵树就长高了一层。

通过这种“满了就裂，中间提拔”的自动化机制，B树永远能保持自己的平衡，无论数据如何插入，从根到任何一个叶子的路径长度都保持一致，从而保证了极其稳定和高效的查询性能。

*一个不错的比喻就是告诉公路：根节点和分支节点(都是高速公路上的路标指示牌**(节点①和②)** ，它告诉你从哪里下去。叶子节点就是数据节点，就是你要找的目标（包含了回表的指针）：根和树枝是指示牌，叶子是目标，找到目标通过指针回表拿数据。*

说明 ​

  • 树的“阶”和树的“层高”是两个完全不同的概念。
    • 3阶树：说的是它的内部结构规定。它是一个“3户型”的楼，这个规定永不改变。
    • 3层高：说的是它当前的状态。它目前是一栋3层楼高的建筑。
  • 树的层高是会随着数据的增多而动态变化的。 一开始数据少，可能只有1层（只有根节点）。数据多了，就会变成2层、3层……那数据越来越多，层数越来越高，查询不是会变慢吗？这就是B树被称为“矮胖”的原因，也是它如此高效的关键。在真实的数据库中，B树的“阶”数非常大，不是我们为了演示用的3阶，而可能是几百阶！这带来的结果就是：树的高度增长得极其极其缓慢。一个只有3到4层高的B树，就可以轻松地存储上亿条记录。当你查询时，从上到下只需要经过3-4个节点，这在计算机看来几乎是瞬时完成的。

B 树范围查询为什么高效？ ​

  • 数据在所有层面都是有序的
  • 最底层的叶子节点之间是相互连接的。
markdown
**## 一次高效的树查找 + 一次高效的水平扫**

目标：找到年龄在 20 到 30 之间的人。第1步：快速定位范围的“起点” (age ≥ 20) B树不会从头扫描，而是利用树形结构进行高效的“跳查”，就像我们查字典先翻到首字母一样。

- 从根节点 [17] 开始：20 大于等于 17，所以向右走。
- 到达分支节点 [17, 32]：20 介于 17 和 32 之间，所以走中间那条路。
- 到达叶子节点 [17, 21]：我们到达了最底层！数据库在这个节点里扫描，找到了第一个大于或等于20的值：21。
- 通过21后面的指针，它立刻找到了ID为1007的数据行，并将其加入结果集。

找到了第一个符合条件的数据 21 之后，数据库不需要再从根节点开始查找下一个了。因为B树的叶子节点就像一条串起来的链子，[17, 21]这个节点“知道”它的下一个邻居是[32, 60]这个节点。数据库直接水平移动到下一个叶子节点 [32, 60]，数据库检查新节点 [32, 60] 的第一个值：32，它发现32已经大于我们范围的上限30了，因为叶子节点的数据是严格有序的，所以数据库可以立刻确定：后面的所有数据都肯定不符合条件了。查询立即终止。它避免了对整张表的扫描，仅仅只访问了索引中包含目标数据的一小部分，以及数据表中那几条真正符合条件的行。这就是B树范围查询高效的根本原因。